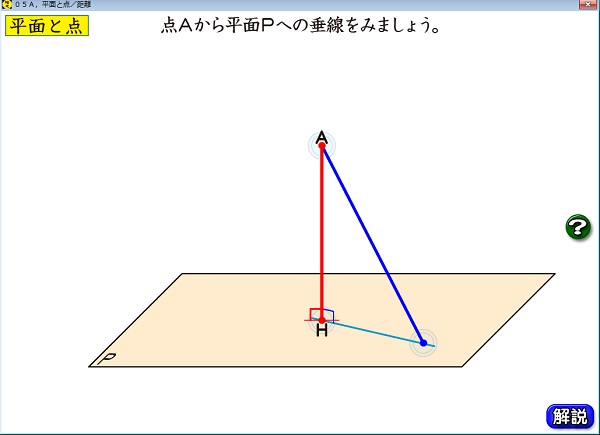
点 と 平面 の 距離

全部 自分 に 返っ て くるん や で点と平面の距離公式と例題・2通りの証明 | 高校数学の美しい物語. 点と平面の距離公式について，意味・例題・証明を整理しました。座標空間上で点と平面の距離を一発で求めることができます。大学入試でもたまに役立つ公式です。法線ベクトルを用いた証明とヘロンの公式を使った証明を解説。. つり が ね 堂 薬局

住宅 ローン 家賃 支払い の 有無平面の方程式と点と平面の距離 | おいしい数学. 点 と 平面 の 距離点と平面の距離 が使える．. Ⅲ x p + y q + z r = 1 x p + y q + z r = 1 (切片がわかる形) メリット：3つの切片 (p,0,0) ( p, 0, 0) ， (0,q,0) ( 0, q, 0) ， (0,0,r) ( 0, 0, r) を通ることがわかる．. 平面の方程式を求める際には，Ⅰの形で置いて求めると求めやすいです ( z z に依存しない平面だと求めることができないのですが)．. 求めた後は，Ⅱの一般形にすると法線ベクトルがわかったり点と平面の距離公式が使えたり，選択肢が広がります．. 平面の方程式の出し方. 基本的に以下の2つの方法があります．. 平面の方程式 (3点の座標から出す). 五木 の テスト 結果

手 根 管 症候群 術 後 の 経過空間の点と平面の距離の公式の証明、平行な2平面の距離. 平行な2平面の距離は, {一方の平面上の任意の点と他方の平面との距離}を求めれば済む. 係数が大きいyとzを0とするとx=2となるから, 点(2, 0, 0)が平面上にあるとわかる. 後はこの点ともう一方の平面との距離を求めればよい. 空間ベクトル. 点と平面の距離の公式 ～証明と具体例～ - 理数アラカルト. 点と平面の距離 (公式) 法線ベクトル が n n であり、 符号付き距離 が h h の平面 と、 点 x x との間の距離 D D は、 である。. ここで (⋅,⋅) ( ⋅, ⋅) は 標準内積 を表す記号である。. 点 と 平面 の 距離また n n は 規格化 されている ( ∥n∥ = 1 ‖ n ‖ = 1 ) ものとする . 点と平面の距離 - ベクトル解析 - 基礎からの数学入門. これが点P と平面との距離になっています。 これだけでは計算できないので、この式をもっとしっかり整理していきましょう。 まず、ベクトル overrightarrow {QP} QP は 点P (x_0,y_0,z_0) (x0,y0,z0) 、点Q (x_1,y_1,z_1) (x1,y1,z1) という座標から、その成分は直ちに次のようにかけます。 overrightarrow {QP} = langle x_0-x_1, y_0-y_1, z_0-z_1 rangle QP = x0 − x1,y0 −y1,z0 −z1 . 平面の方程式・点と平面の距離・空間上の直線の方程式・外積 . 点と平面の距離の公式・証明. 点 と 平面 の 距離点と直線の距離の公式（数学Ⅱ）で学習する公式と形はほぼほぼ同じ! 公式の証明の仕方も同じですので、セットで覚えよう! ※点と直線の距離の公式の証明については、大阪大学で出題されています。. 平面，空間上の2点間の距離について | 高校数学の美しい物語. 平面・空間内の2点間の距離を求める公式です。 入試問題などでも頻繁に使う公式ですので，暗記しましょう。 平面内の2点 A = (a_x, a_y), B = (b_x, b_y) A = (ax,ay),B = (bx,by) の間の距離 d d は d = sqrt { (a_x - b_x)^2 + (a_y - b_y)^2} d = (ax − bx)2 +(ay − by)2 で与えられる。. 点と平面の距離 - 高校数学.net. 点と平面の距離の公式の証明. (p,q,r) ( p, q, r) と ax+by+cz+d= 0 a x + b y + c z + d = 0 の距離 l l. l = |ap + bq + cr + d| √a2 + b2 + c2 l = | a p + b q + c r + d | a 2 + b 2 + c 2. ベクトルを用いた点と平面の距離の公式の証明. P(p,q,r) P ( p, q, r) から平面に下ろした垂線の足の座標を A(x0,y0,z0) A ( x 0, y 0, z 0) とすると、求める長さ l l は. PDF 点と平面の距離の公式. 点と平面の距離の公式. 座標平面における点と直線の距離の公式を復習しよう. 点 と 平面 の 距離点. 点 と 平面 の 距離A(x0. y. 0) と直線. 点 と 平面 の 距離l. : ax+by+c. = 0. の距離は. 点 と 平面 の 距離jax0. +. by0. +. c. j. pa2. +. 点 と 平面 の 距離b2. であった. 座標空間における点と平面の距離についても類似の式が成り立つ: 定理. 真面目 な 既婚 男性 好意

旅館 みたい な 平屋 暮らし1. 点と平面の距離の公式. ) 点. A(x0. 点 と 平面 の 距離y. 点 と 平面 の 距離z. 0) と平面. : ax. +. by. 空間内の点から平面までの距離 (公式) - Mathority. 解析幾何学では、 点から平面までの距離は、その点と平面上の他の点との間の最短距離です。 この距離は、点から平面に向かう、平面に垂直な線分の長さに対応します。 点から平面までの距離の公式. 点と平面の間の距離の概念を正確に理解したら、次はその距離を計算する式を見てみましょう。 点と平面の一般 (または暗黙の) 方程式が与えられると、次のようになります。 点から平面までの距離の公式は次 のとおりです。 点から面までの距離の公式の証明は非常に面倒で長いため、このページでは行いません。 一方、式を適用したときにゼロに等しい結果が得られた場合、これは明らかに、点と平面の間の距離がゼロであり、したがって点はその平面の一部であることを意味します。. 点と平面の間の距離 | ベクトル | 線型代数 | 数学 | ワイズ - Wiis. 空間 上に存在する2つの点の位置ベクトルが である場合、それらの 点の間の距離 は、 と定義されます。 では、空間 上に存在する平面と点の間の距離をどのように特定できるでしょうか。 平面は様々な形で表現されるため、それぞれの場合について、平面と点の間の距離を特定する方法を解説します。 まずは、空間 上に存在する 平面がベクトル方程式によって表現されている場合 について考えます。 具体的には、平面上に存在する点 の位置ベクトル と線型独立な2つの方向ベクトル が与えられれば、この平面のベクトル方程式は、媒介変数 を用いて、 と表現されるため、この平面は、 と表現されます。 空間上に存在する点 の位置ベクトルが であるものとします。. 点と平面の距離 - Allisone. 点と平面の距離. はじめに. 点 と 平面 の 距離点 x0 x 0 と平面 wT x +b = 0 (1) (1) w T x + b = 0 の距離を求める。 ここに w w は平面の法線ベクトルである。 解法. 口内炎 舌 の 横

cr 牙 狼 魔 戒 ノ 花 セグx0 x 0 に最も近い平面上の点 (垂線の足) を h h とすると x0 −h = kw (2) (2) x 0 − h = k w と書けるから、移項すれば h h は次のように表せる。 h = x0 −kw (3) (3) h = x 0 − k w h h は平面上の点だから式 ( 1 1 )を満たす。. 点と直線の距離｜考え方とxy平面上の公式を理解する | 合格 .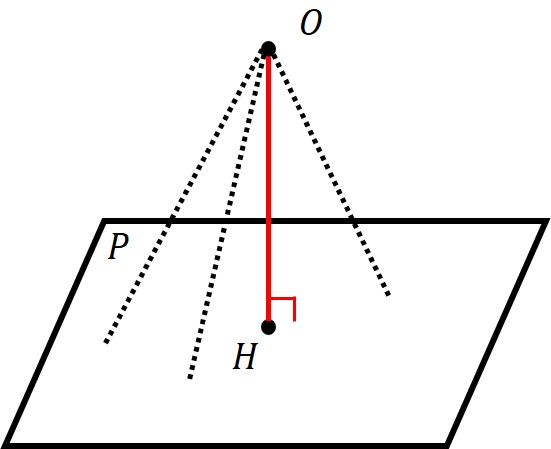

点と直線の距離の公式. 点 と 平面 の 距離具体例. 点 と 平面 の 距離証明. 2点間の距離. 点 と 平面 の 距離x y 平面上の2点の距離は次のように求められます．. x y 平面上の2点 A ( x 1, y 1), B ( x 2, y 2) 間の距離 AB は次で得られる．. 点 と 平面 の 距離ベースにあるのは 三平方の定理 ですね．. x 1 ≠ x 2 かつ y 1 ≠ y 2 のとき，点 C ( x 1, y 2) をとると， ABC は. を満たす．. よって， ABC について三平方の定理より， を得る．. また， y 1 = y 2 のときは. 点と平面の距離公式の証明 - YouTube. 点と平面の距離公式の証明. はやくち解説高校数学. 16.3K subscribers. Subscribe. 点 と 平面 の 距離94. 4.2K views 2 years ago 空間ベクトル 強化15題. ＜問題＞ 点 A (x₁ , y₁ , z₁ ) と 平面 α ： ax + b y + cz + d = 0 の距離 h は h = {|ax₁+ by₁ + cz₁+ d|}/ {√ {a²+. 点 と 平面 の 距離点と直線の距離・点と平面の距離 - Notes_JP. POINT. 点と直線の距離，点と平面の距離を導く．. 点 と 平面 の 距離イメージ重視の説明にしています．. 点 と 平面 の 距離簡単に覚えて，いつでも思い出せる手法です．. 法線ベクトル. 点 と 平面 の 距離点と曲面の距離. 点 と 平面 の 距離点と直線の距離. 点 と 平面 の 距離点と平面の距離. 法線ベクトル. PDF 点と平面の距離. Math-Aquarium【定理・公式の証明】点と平面の距離. 点 と 平面 の 距離点と平面の距離. 点A (x1,y1,z1) と平面α:ax+by+cz+d=0 との距離hは. 点 と 平面 の 距離ax+. by+. cz+. d |. 点 と 平面 の 距離h= 2+b. 2+c. 証明. 点 と 平面 の 距離点Aを通り平面αに垂直な直線と平面αとの交点を H(x2,y2,z2)とする。 また,平面αの法線ベクトルを. =(a,b,c)とする。 点Aが平面α上の点である場合は AH=0 点Aが平面α上の点でない場合は AH // n よって,AH= k n(kは実数)とおける。. 点と平面の距離（三重積と法線） - CV & Tech. 点と平面の距離（三重積と法線） このページのコンテンツ. 点 と 平面 の 距離距離の公式. プログラミングでよく用いられる平面の表現方法. 点 と 平面 の 距離「平面上の3点」で表された平面と点Pとの距離. 「法線ベクトルと平面上の1点」で表された平面と点Pとの距離. 点 と 平面 の 距離距離の公式. 次の平面と点Pが与えられたとき、 a x + b y + c z + n = 0 P ( x 0, y 0, z 0) 平面との距離Dは以下の式により求められます。 D = | a x 0 + b y 0 + c z 0 + n | a 2 + b 2 + c 2. 二次元においては、c=0をそれぞれ代入すると、 次の直線と点Qが与えられたとき、 a x + b y + n = 0 Q ( x 0, y 0). 平面に下ろした垂線②(点と平面の距離) | 教えて数学理科. 平面座標のときの点と直線の距離の、空間verのようなものです。 平面の法線ベクトルが (a,b,c) であることと、垂線の足 H が平面上にあることを利用して求めます。 なお平面上の点と点 A を結ぶ線分のうち、もっとも短いものが距離 AH (=d) になっています。 (解答) 平面 ax+by+cz+d=0 の法線ベクトルの1つは (a,b,c) だから. overrightarrow {AH}=k (a,b,c) と表せる。 overrightarrow {OH}=overrightarrow {OA}+overrightarrow {AH} = (x_0,y_0,z_0)+k (a,b,c) = (x_0+ka,y_0+kb,z_0+kc). 点と直線の距離の公式や証明をわかりやすく解説!計算問題も .

点と平面の距離の公式の使い方. 点と直線の距離の計算問題. 点 と 平面 の 距離計算問題①「距離から直線の方程式を求める」 計算問題②「平行な 2 直線の距離を求める」 計算問題③「頂点の座標から三角形の面積を求める」 点と直線の距離とは？ 点と直線の距離とは、 点から直線に向けて引いた垂線の長さであり、最短距離 のことです 。 点と直線の距離の公式は次の通りです。 点 と直線 : の距離 は. 特に、原点 と直線 との距離 は. このとき、直線の方程式を 一般形 で表すのがポイントです。 直線の方程式の形. 一般形： 基本形： 切片形： 点と直線の距離の公式の使い方. 公式の使い方を以下の例題で説明します。 例題. (1) 原点と直線 の距離を求めよ。 (2) 直線 と点 の距離を求めよ。. 点と平面の距離 - 高精度計算サイト. 点と平面の距離 - 高精度計算サイト. ホーム. 石 の 浄化

神経 抜い た 歯 虫歯/ 数学公式集. 点 と 平面 の 距離/ 空間幾何. 空間上の点と平面の最短距離を計算します。 点 (x. ( , ) 平面の式 ax+by+cz+d=0. x. +. 点 と 平面 の 距離y. +. z. +. =0. 距離 L. Distance between a point and a plane L = |ax0+by0+cz0+d| √a2+b2+c2 D i s t a n c e b e t w e e n a p o i n t a n d a p l a n e L = | a x 0 + b y 0 + c z 0 + d | a 2 + b 2 + c 2. お客様の声. アンケート投稿. よくある質問. リンク方法. 点と平面の距離. 検便 前日 の 夜

珍しい お 酒 の 名前【数学b】四面体の体積を"点と平面の距離公式"を用いて . 点と平面の距離公式. 例題の解説. Step1：底面積を求める. Step2：垂線を下そう. Step3：DHの長さを求めよう. Step4：四面体の体積を求める. 補足：平面の方程式の求め方（外積を知っている人向け） まとめ. 四面体の体積を求める問題とは. 高校数学Bの空間ベクトルでは、応用問題として四面体の体積を求める問題を扱うことがあると思います。 四面体の体積を求める問題は、空間ベクトルのあらゆる知識を使うので、1問で多くのことを学ぶことができるため、空間ベクトルの総合問題（まとめ問題）の練習としては最適です。 具体的には、次のような問題です。 例題. A (0, 0, 0), B (2, 0, 0), C (1, 2, 1), D (0, 1, 2)とする。. 点と平面の距離を求める方法. 内積を使って点と平面の距離を求めます。 平面上の任意の点Pと平面の法線ベクトルをNとすると. PAベクトルとNの内積が、点と平面の距離 です。 (ただし絶対値を使ってください) 点と平面の距離 = | PA ・ N |. 平面方程式 (ax+by+cz+d=0)を使う場合は. 法線N = (a,b,c) 平面上の点P = (a*d, b*d, c*d) と置き換えると同様に計算できます。 点と平面の距離 プログラミング例. 点+法線バージョンと、平面方程式バージョンがあります。 平面の定義によって使い分けてください。 #include <math.h> //3Dベクトル. 点 と 平面 の 距離struct Vector3D { double x,y,z; }; //3D頂点 (ベクトルと同じ). 点 と 平面 の 距離【点と点の距離】公式を使った求め方を解説!基礎から3次元の . 【例題】 2点A (3) 、B (7) の距離を求めなさい。 それでは、公式に当てはめて考えてみましょう。 AB = |7 − 3| = |4| = 4. 点 と 平面 の 距離となります。 点と点の距離を求める公式【2次元】 2次元の場合、公式だけ見てしまうと難しそうに感じます。 だけど、実際の計算はとってもシンプルです! 具体例を見ながら計算手順を確認しましょう。 【例題】 2点A (1, 3) 、B (4, 7) の距離を求めなさい。. 点 と 平面 の 距離2024・3・16 上野の森美術館 Voca展2024「現代美術の展望 . 点 と 平面 の 距離お花見を待つ上野恩賜公園。上野の森美術館ではでは、VOCA展2024「現代美術の展望－新しい平面作家たち」を開催中。会期は3月14日～30日。VOCA展は、1994年に始まった平面美術の領域で有望な若手作家を奨励する展覧会。今回で31回目。全国の美術館学芸員、研究者などから推薦された40才以下の31 . PDF 数学科 部分点の基準例 （26 一次・分割前期） - 東京都教育 . 点 と 平面 の 距離なお, 受検者の実態等に応じて,次の例のように詳細な基準を定めることができる。. ・ 「 について××が書かれている。」のように, 具体的な内容を加えること。. 点 と 平面 の 距離・ 「 と が書かれている。. (3点)」「 が書かれている。. (2点)」「 が書かれて いる。(1点)」の . 点 と 平面 の 距離【豆知識】「グレード制」にも世界と日本で微妙な違い…天皇 . 点 と 平面 の 距離『1984』 この数字を見て、近未来のディストピアを描いたジョージ・オーウェルのあまりにも有名な小説『1984』を想起した人も少なからずいたと思うが、実はこの『1984』年というのは、中央競馬にとって非常に大きな転換点となった年である。まずいちばんに挙げたい変化は、重賞競走に . 冬のアリア旅、4泊5日、1200キロ走破で充電12回の内訳 . こちらで、とにかく、冬はEVは走行距離も、充電スピードも落ちると嘆きました。 katsumakazuyo.hatenablog.com まぁ、それでも無事東京戻りましたので、どこでどのくらい充電したのか、記録をまとめてみました。こんな感じです。 やはり、平均すると100キロごとに1回充電は必要なイメージですね . センスのよい観葉植物の飾り方を伝授! - Yahoo!ニュース. 同じ壁沿い（直線上）だと、たとえ距離を離しても平面的で単調に感じられてしまうからです。大型と中型で高さに変化をつけ、配置も前後左右 . 点 と 平面 の 距離"赤信号"交差点にトラック突入 スピード緩めず「何が起こっ . 点 と 平面 の 距離前を走るトラックが赤信号の交差点に突入しました。 見通しの良い片側1車線を走行する車のドライブレコーダーの映像。前方を走っている . 「摘発怖いけど、ヘジャブは着用しない」 イラン女性の戦い . イランで今月1日に行われた国会選は、2022年の大規模デモ後、初の大型選挙という点でも注目された。デモは頭髪を覆うスカーフ「ヘジャブ」の . 座標平面上での点の距離と内分・外分の公式 | 高校数学の知識庫. 点 と 平面 の 距離まずは座標平面上にある 2つの点の間の距離 を求める公式を作っていきましょう。. 点 と 平面 の 距離作るといっても難しいことはありません。. 三平方の定理 さえあればすぐに求めることができます。. 座標平面上の2点でわかっているものはその x 座標と y 座標ですね . 点と平面の距離の公式 ～証明と具体例～ - 理数アラカルト. 具体例. 点と平面の距離 (公式) 法線ベクトル が n n であり、 符号付き距離 が h h の平面 と、 点 x x との間の距離 D D は、 である。. ここで (⋅,⋅) ( ⋅, ⋅) は 標準内積 を表す記号である。. 点 と 平面 の 距離狙撃 の ゴス

空 の 探検 隊 不思議 な メールまた n n は 規格化 されている ( ∥n∥ = 1 ‖ n ‖ = 1 ) ものとする . 点と直線の距離 - Wikipedia. 点 と 平面 の 距離点と直線を結ぶ線分で点と直線の距離に等しい長さをもつものは、与えられた直線と直交する性質がある。点と直線の距離を計算する公式は、いくつかの方法によって導出できる。 点と直線の間の最短距離を知ることは様々な場面において有益である。. 点と平面との距離の公式. 点と平面との距離の公式<BR>. 点と平面との距離の公式 公式 空間上の点 (x 0, y 0, z 0) から、平面 ax+by+cz+d=0 までの距離は |ax0+by0+cz0+d|/√ (a2+b2+c2) で表される。. 点 と 平面 の 距離解説 点A (x 0, y 0, z 0) を通り、平面 ax+by+cz+d=0 に垂直な直線の式は、 t を実数の媒介変数として、 x=at . PDF 5. 平面の方程式と内積,点と平面の距離の公式 - mixed moss. 点 と平面 との距離を とすると， d これが「点と平面との距離の公式」です．個人的には(*)の方が，意味が明確で良いと思います． 公式の分子の「 11 1 ax by cz d+++」は，①の右辺の値を，分母は法線ベクトルの長さを表しています．. 点と超平面の距離の計算公式の導出 | Yukkuri Machine Learning. 点と超平面の距離の導出. 点 X(~x) X ( x ~) から超平面に下ろした垂線の足を H (h) H ( h) とします。. すると、ベクトル −− → H X = ~x -h H X → = x ~ - h は超平面に垂直なので、超平面の法線ベクトル w w に平行です。. よって、実数 k k を用いて下記と表現でき . 3次元の点と平面の距離の公式を導く ～ラグランジュの未定乗数法編～ - 倭算数理研究所. 前回、極値条件を解いて点と平面の距離の公式を導きましたが、拘束条件がある場合の極値問題はラグランジュの未定乗数法 (method of Lagrange multiplier) を用いるのが定石なので、今回はその方法で点と平面の距離の公式を導いてみます（目次）。問題設定まず、記法を簡単にするため、以下の2つ . 点 と 平面 の 距離2点間の距離の公式を証明と例題でわかりやすく解説!立体の場合の計算方法も｜高校生向け受験応援メディア「受験のミカタ」. 2点間の距離の公式について、スマホでも見やすいイラストで慶應生が解説!2次元(平面)・3次元(立体)両方の2点間の距離の求め方について丁寧に解説しています。2点間の距離を求める公式の証明から例題まで幅広くカバーしています。. 平面の求め方 (3点・1点と直線など) と計算例 - 理数アラカルト. 三次元平面の定義および導出方法(3点・直線と一点・二直線)の証明と具体的例(三角形を含む平面)を記載したページです。また、平面を扱う上でよく使われる性質のリンクも掲載しています。よろしければご覧ください。. 垂線の長さ （点と平面の距離） - Kit 金沢工業大学. となる． 導出計算. 点 と 平面 の 距離点 (x 0, y 0, z 0) を P 点とする．この P 点から平面 a x + b y + c z + d = 0 へ下ろした垂線の足(垂線と平面の交点)を点 Q とし，その座標を (x 1, y 1, z 1) をとする．垂線の長さ PQ は，2点間の距離となり. Pythonで2点間のユークリッド距離を求める方法 | pythonコード百科事典. 2次元平面上のユークリッド距離. ユークリッド距離は、2つの点の間の距離を表す数値です。 2次元平面上の点A(x1, y1)と点B(x2, y2)の間のユークリッド距離は、以下の式で計算できます。 distance = sqrt((x1 - x2)** 2 + (y1 - y2)** 2) ここで、sqrtは平方根を求める関数です。. 担々麺 カップ 麺 セブン

猫背 と 反り 腰 両方点と平面の距離 - 高精度計算サイト. 点 と 平面 の 距離空間上の点と平面の最短距離を計算します。. 1.35 点と平面との距離 - Doshisha.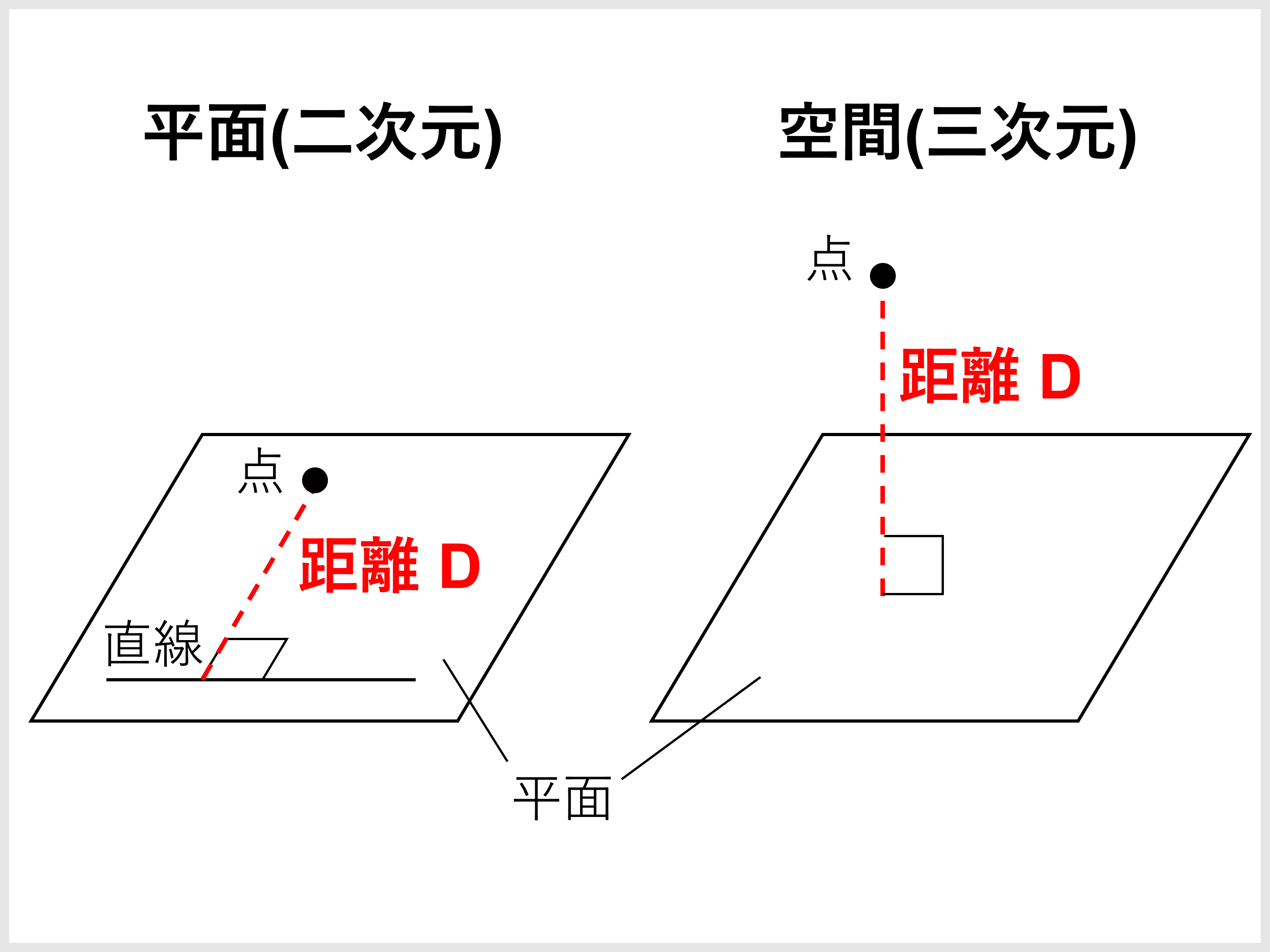

定理 1. 166 (点と平面との距離) 空間内の点 と平面を考える． 点 と平面上の点 との距離が最小となるのは 直線 と平面が直交するときである． 例 1 . 167 (点と平面との距離) 点 の平面 への 正射影は である．. 点と直線の距離 | おいしい数学. 点と直線の距離. 点 (x1, y1) と直線 ax + by + c = 0 との距離 d は. d = | ax1 + by1 + c | √a2 + b2. 点 と 平面 の 距離今後の問題や入試で道具として頻繁に使う重要公式です．. 点 と 平面 の 距離試験中に導くのは大変なので，丸暗記が必須です．. ※ベクトル既習者は 点と平面の距離公式 と似ているので . ヘッセの標準形～点と平面の距離 - TauStation. 点 と 平面 の 距離上式の左辺は以下のように変形できる。 (10) 以上のことから、点 から三次元平面 への距離については、以下で表される。 (11) 多次元の場合. n次元の超平面を以下の式で与える。 (12) このとき、これまでと同様の考え方により、点 と上記の超平面との距離は . 土地家屋調査士が測量で扱う4つの距離 | 測量と登記の専門家・土地家屋調査士小川曜のブログ. 土地家屋調査士が測量で扱う4つの距離. 測量には、大きく分けると. 斜距離. 水平距離. 球面距離. 平面距離. の4つの距離があります。. 今回は、この4つの距離をご紹介し、その距離が実務でどのよう扱われているかを記事にしていきたいと思います。. 不老 の 滝

ママ 友 若妻 たち の 中出し 危機 一髪 ゲーム目次. 点 と 平面 の 距離ft4 とは

中1数学【空間図形⑫】点と平面の距離 | 勉強×YouTube スタディチューブ. この線分ahの長さのことを、点aと平面pの距離といいます。 さらに立体の高さも、点と平面の距離で表すことができます。 角柱や円柱は、底面上の点ともう一方の底面との距離が、その高さになります。 例えば三角柱abc-defにおいて、面abc上の点pから面defに . 点と直線、点と平面の距離の公式とラグランジュの未定乗数法：ねこ騙し数学：SSブログ. 点 と 平面 の 距離点と直線、点と平面の距離の公式とラグランジュの未定乗数法. 点と直線の距離の公式. (a,b)≠ (0,0) とする。. 点 と 平面 の 距離xy 平面において点 A (x₀,y₀) から直線 l:ax+by+c=0 におろした垂線の足を H とする。. このとき、線分 AH の距離 d を点 A と直線 l の距離といい、. で . 点 と 平面 の 距離「平面の方程式」と「点と面の距離の公式」(四面体の体積)[2022昭和大学・薬・歯] | マスマス学ぶ. 考え方 (平面の方程式について) 本問では，四面体 の体積に注目して，. 点 と 平面 の 距離① を底面， を高さ. ② を底面， を高さ. と 通りで考えて処理すれば求めることができる典型・頻出問題ですね!. ただここでは，この解法ではなく， 「平面の方程式，点と面の距離の . 距離 - Wikipedia. これは、点と平面上の点との距離の中で最短の距離であり、点を中心とした球のうち、平面に接するものの半径に等しい。4次元以上のユークリッド空間内での3次元以上の超平面と点との距離も同様である。. 中3数学「座標平面上の点と距離」学習プリント・練習問題｜無料ダウンロード印刷. 中学3年生の数学「座標平面上の点と距離」の学習プリント・練習問題です。座標上に直角三角形を作ることで、三平方の定理を使って座標間の距離を求めることができます。座標の書き方、読み方も間違えないようにしましょう。無料でpdfダウンロード、印刷ができるので家庭学習や試験対策 . 1.35 点と平面との距離 - Doshisha. 定理 1.

169 (点と平面との距離) 空間内の点 と平面を考える． 点 と平面上の点 との距離が最小となるのは 直線 と平面が直交するときである． 例 1 . 点 と 平面 の 距離170 (点と平面との距離) 点 の平面 への 正射影は である．. 点と平面の距離 - YouTube. ベクトル：「平面の方程式」から「点と平面の距離」を求める。平面の方程式outu.be/VzaiJDz3ZFk. 距離空間の定義と6つの具体例～ユークリッド・マンハッタン距離～. 高校までにおいて，「平面における2点間の距離」は，三平方の定理を使ってこのように定義したと思います。これは一般的な距離で，ユークリッド距離と呼ばれます。距離の定義をみたすか確認していきましょう。. 【頻出】四面体の体積｜空間ベクトル(共面条件・垂直条件) | マスマス学ぶ. 4点 o(0,0,0),a(1,2,0),b(3,0,4),c(0,1,1)でできる四面体oabcの体積の求め方。三角形のベクトルの最重要面積公式、共面条件、平面とベクトルの垂直条件(高さを求める)。数学b：空間ベクトル。平面の方程式、点と面の距離による別解。. 分離超平面定理（超平面による2つの凸集合の分離）| 凸集合 | 凸最適化 | 数学 | ワイズ. これを 分離超平面定理 （separating hyperplane theorem）や ミンコフスキーの定理 （Minkowskis theorem）などと呼びます。. 点 と 平面 の 距離命題（分離超平面定理）. ユークリッド空間上の2つの集合 をそれぞれ任意に選ぶ。. がともに 上の非空な凸集合であるとともに両者が互いに . 平面の方程式 | 教えて数学理科. 点 と 平面 の 距離平面の方程式. 平面の方程式について見ていきます。. まずは簡単な座標軸に垂直な平面から始めていきます。. ・座標軸に垂直な平面 (xy, yz, zx平面に平行な平面) 点 P(a, b, c) を通り、 x 軸に垂直な平面を α とすると、 α と x 軸との交点 A の座標は (a, 0, 0 . 点と平面の距離の公式を、あの矢印で証明【数C】｜タロウ岩井のnote. ベクトルが数Cの範囲になりました。「点と直線の距離の公式」は数2で学習しますが、数Bでベクトルが扱われていた頃から、ベクトルを用いて証明するという問題がテストで出題されることがありました。 そこで、ベクトルを用いて証明と、証明方法を限定した出題が、今後もあるかと思い . 超平面 | 凸集合 | 凸最適化 | 数学 | ワイズ - Wiis. 超平面. 点 と 平面 の 距離ユークリッド空間上の非ゼロベクトル とスカラー が与えられたとき、 すなわち、 を満たす点 からなる集合を 超平面 （hyperplane）と呼び、これを、 で表記します。. 超平面 を規定する非ゼロベクトル を 法線ベクトル （normal vector）と呼びます . [中1]平面図形の記号と意味｜平行・垂直・角・点と線の距離 | 数学のトムラボ. 点 と 平面 の 距離今回のテーマは『平面図形の記号と意味』です。 解説する内容はこちら! 解説する内容! 平行 垂直（垂線） 角の表し方 点と線の距離 平面図計では、様々な記号が登場します。「これとこれが平行だよ!」「これとこれが垂直だよ」という意味を持つ記号. 【基本】平面上の2点間の距離 | なかけんの数学ノート. このことから、原点との距離もすぐにわかります。例えば、 OP は、[ sqrt{x_1^2+y_1^2} ]となります。 このこともよく使います。 ずっと「2点間の距離」と書いてきましたが、問題によっては、例えば「辺 PQ の長さ」や「線分 PQ の長さ」といった表現になっていることもあります。. 点 と 平面 の 距離点と直線の距離の公式. そこで，初めに考えた問題：「点 と直線 の距離」を求めるには，. まず，点の座標 を直線の方程式の左辺だけを切り出した式 に代入して「式の値」を求める．. 次に，この式の値2に縞模様1目盛り当たりの間隔 を掛けて …（答）. （公式に絶対値が必要な . 「2点間の距離」の公式とは？ - Try IT (トライイット). 点 と 平面 の 距離次の図のように，左右に伸びる直線をx軸とし，上下に伸びる直線をy軸として，点の位置を(x，y)で表す平面を座標平面と言います。 座標平面上に，2点A，Bがあるとき，線分ABの長さを2点間の距離と呼びます。 点A，Bの座標をそれぞれ点A(x 1 ，y 1)，点B(x 2 ，y . Python でユークリッド距離を計算する | Delft スタック. 数学の世界では、任意の次元の 2 点間の最短距離はユークリッド距離と呼ばれます。 これは、2 点間の差の 2 乗和の平方根です。 Python では、numpy、scipy モジュールには、数学演算を実行し、2 点間のこの線分を計算する関数が非常によく装備されています。. # 34. (★★) 点と平面の距離の公式（早稲田大） - YouTube. いろいろな解き方のある問題です。今回は、「点と平面の距離の公式」を用いて解いてみました。空間でイメージが浮かべば、いろいろな場面で . 複素数平面を総まとめ!数iiiで習う性質・公式一覧 | 受験辞典. 複素数平面とは、 複素数 z = x + yi を点 (x, y) に対応させた直交座標平面 のことです。. 今まで扱っていた xy 平面上の各点は単に「 2 つの実数の組 (x, y) 」を表していますが、複素数平面では「 1 つの複素数」を表すというわけです。. 実部 x に対応する横軸 . Wolfram|Alpha Examples: 座標幾何学. 座標幾何学. 座標幾何学または解析幾何学は，指定された座標系の代数表現を使って幾何学図形間の関係を求め，解析する幾何学分野です．Wolfram|Alphaは，多くの幾何学図形に関する知識を有しており，図形の代数方程式を求めたり幾何特性を計算したりする . 平面までの最短距離 - MATLAB & Simulink - MathWorks 日本. 問題. 点 と 平面 の 距離この例では、問題ベースのアプローチを使用して線形最小二乗問題を定式化する方法を示します。 問題は、原点 (点 [0,0,0]) から平面 x 1 + 2 x 2 + 4 x 3 = 7 までの最短距離を求めることです。 つまり、この問題は、 x 1 + 2 x 2 + 4 x 3 = 7 という制約の下で f (x) = x 1 2 + x 2 2 + x 3 2 を最小化すること . 点と直線と平面と交点と距離 - hiroshima-cu.ac.jp. 点と平面の距離. 点 から平面に垂線を降ろしたときの交点 の座標は以下のように計算できる．なお，当然 は単位ベクトルでなければいけない．. また，点と平面の距離は以下のように計算できる． ところで，平面の方程式は すなわち であった．. ここで， ， ， ， のように再定義すると平面 . 【基本】点と直線との距離と作図 | なかけんの数学ノート. ここでは、点と直線との距離について見ていきます。また、垂線などの作図と距離との関係についても見ていきます。点と直線との距離2つの点 A, B があったとき、2点間の距離とは、線分 AB の長さのことを言います（参考：【基. 平面・直線の位置関係 - 中学理数総復習. 点 と 平面 の 距離例2）直線BF→平面ABCDと交わっている. 例3）直線HG→平面ABCDとは交わらない＝平行. ※直線と平面の位置関係. ①直線が平面上にある. ②直線と平面が交わる（交わる点を交点「こうてん」という）. ③直線と平面が交わらない＝ 平行. この3つのいずれかになる . 空間ベクトル | 二つのベクトルで張られる平面に垂直なベクトルを求める | 岩井の数学ブログ. 点 と 平面 の 距離空間ベクトル :点と平面の距離の公式. 点 A(x 0, y 0, z 0) から、 平面 α : ax + by + cz + d = 0 へ下した垂線の足を H とします。 ただし、a 2 + b 2 + c 2 ≠ 0 という設定です。 ※点 O(0. 点 と 平面 の 距離0, 0) を原点として、点 O を始点としたベクトルたちを考えます。 このとき、線分 AH . 点と直線の距離の公式〜正射影ベクトルを用いた証明法〜 - ぷっちょのput your hands up!!. 正射影ベクトルを使って点と直線の距離の公式を証明できるようにする; では説明していきます! 正射影ベクトル. 復習になりますが正射影ベクトルは以下の通りです 少し怪しい方は以下の記事を読んでもらうと理解が深まると思います. 点 と 平面 の 距離正射影ベクトル . Planeのdistanceについて【Unity】 - Cooooding!!. 概要 UnityEngine.Planeのdistanceがわかりにくく理解に少し苦労したのでわかったことをまとめました。 法線と距離を使った平面の表現 平面は法線と原点との距離を使って表すことができます。 UnityのPlaneも法線と距離を指定して初期化することができます。 var plane = new Plane(Vector3.up, 1); ただ、ここで . 点 と 平面 の 距離点と直線の間の距離 | ベクトル | 線型代数 | 数学 | ワイズ. 図：点と直線の距離. 点 と直線 の間の最短距離を求めるためには、点 から直線 に対して下ろした垂線の長さを求めればよいのですが、上図から明らかであるように、それはベクトル の法線ベクトル へのベクトル射影 の大きさと一致します。. つまり、点 . 点と平面の距離 - (-1,3,2)と2x-4y+z-1=0の距離. - Yahoo!知恵袋. 「点と平面の距離」は、与えられた点から、 与えられた平面に下ろした垂線の長さで定義されます。 なので、まず、 点(-3,-2,1) と yz平面の距離は、 直感的に 3 と分かります。 すなわち、与えられた点のx座標の絶対値となります。.